About
In this post, we’ll look at some basic algorithms and data structures in C#.
There are a lot of algorithms and data structures out there. Here I will show you the more common ones I think are worth knowing. There are simply too many of them to learn them all and knowing how to solve all of them off the top of your head is unrealistic. I think when you understand the concepts behind these few basic DSAs you will be able to understand and learn about other DSAs when you actually need to learn them. If you just cram a bunch of stuff into your head and don’t use it for years you will most likely forget it anyway.
It’s more important to know how to solve problems and learn about other algorithms and data structures when the need arises. For example, I have been programming professionally for almost 7 years(at the time of writing) and I just recently needed to learn about force-directed graph drawing(visualization for trees/graphs) as this came up at work. Should you also learn about force-directed graph drawing and a hundred other case-specific algorithms? Probably not and if it ever comes up just learn about it right there and then like I did.
Now I know that a lot of people these days are learning data structures and algorithms to pass the coding interviews. I personally think that these are pointless BS. But if you want to get a job and they require a coding interview well then it doesn’t matter what I think. You’ll just have to try and learn(memorize) a hundred different problems/algorithms and then try to brute-force your way through coding interviews.
Table Of Contents
Data Structures in .NET
public static void RunDotnetDataStructures()
{
//Data structures part of .NET
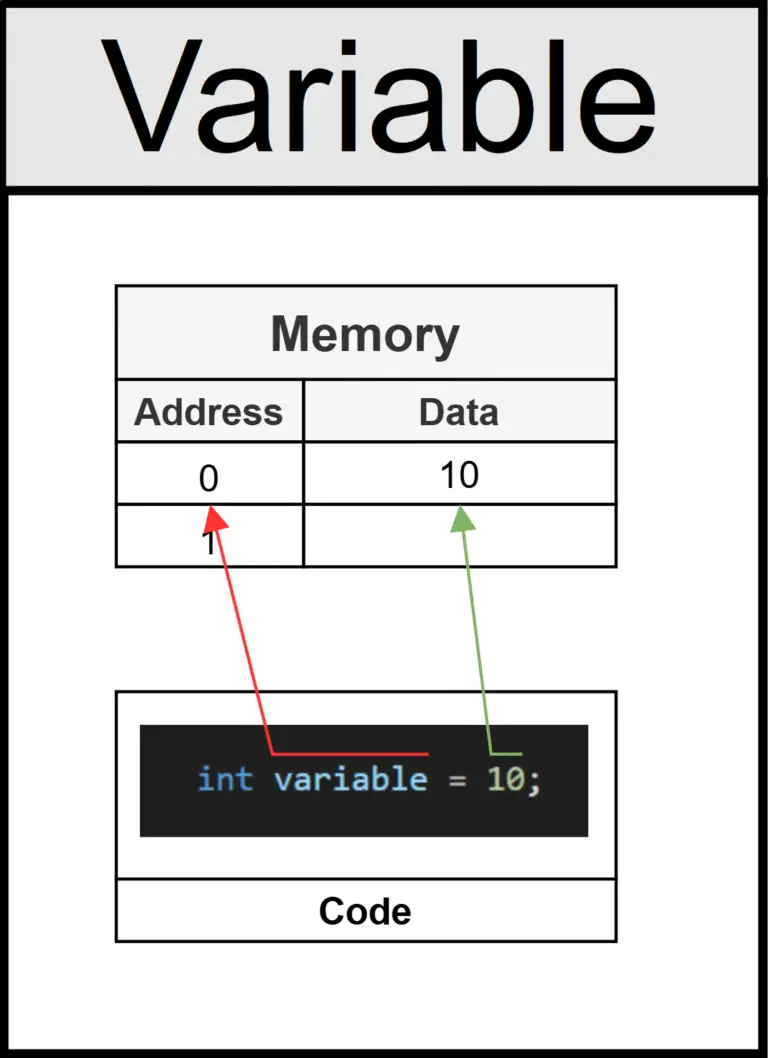
//This is just a regular variable. A single value stored at a memory location.
int variable = 10;
//An array is a collection of values stored in a contiguous(values stored one after the other in memory) chunk of memory.
//In the example below the "array" variable contains the memory location of the first element of the array.
//When you use the index like so "[1]" it's added to the memory location stored in the "array" variable.
//The resulting value is the memory location of where the requested the element is located.
//This makes array lookups very fast, O(1) time complexity.
int[] array = new int[3];
array[0] = 2;
array[1] = 5;
//A list is a collection of values stored in memory(different parts of memory).
//The elements in the list store the value itself and a pointer to the location of the next element.
//This makes a list slower than arrays for lookups, O(n) time complexity.
//But they are much more flexible when it comes to adding/removing elements.
//Unlike arrays they don't have to be resized if the number of elements exceeds the originally allocated size.
List<int> list = new List<int>();
list.Add(8);
list.Add(7);
list.RemoveAt(0);
//A queue contains elements in a FIFO(first in first out) order.
//You can only add elements to the back of the queue(using Enqueue()) and remove elements from the front of the queue(using Dequeue()).
//A queue is really just a list with some restrictions on how you can interact with it.
//The restriction is that you can only add elements to the front of the list and remove them from the back.
Queue<int> queue = new Queue<int>();
queue.Enqueue(1);
queue.Enqueue(5);
queue.Enqueue(3);
int queueItem = queue.Dequeue();
//A stack contains elements in a LIFO(last in first out) order.
//You can only add elements to the top of the stack(using Push()) and remove elements from the top of the stack(using Pop()).
//A stack is also really just a list with some restrictions on how you can interact with it.
//The restriction is that you can only add elements to the front of the list and also only remove them from the front. (you could also do the opposite and only add/remove elements from the back)
Stack<int> stack = new Stack<int>();
stack.Push(1);
stack.Push(5);
stack.Push(3);
int stackItem = stack.Pop();
//A hash set is a collection of unique values with very fast lookup times for stored values.
//This is because it uses a hash function to map the value to a location in memory(just like an array). We'll see how it works when we implement our own later on.
//A typical use case for a hashset would be iterating over a data structure and using the hash set to check if you have already visited a node.
//So every time you visit a node you add it to the hash set, then before you visit the next node you check if it's in the hashset.
HashSet<string> hashset = new HashSet<string>();
hashset.Add("hello");
hashset.Add("world");
hashset.Add("!");
if (hashset.Contains("world"))
{
//Do something ...
}
//A dictionary is a collection of key-value pairs.
//It's almost the same as a hashset with the addition of a value stored "behind" the key which can be used to look up the value said value.
Dictionary<string, string> dictionary = new Dictionary<string, string>();
dictionary.Add("id1", "some value");
dictionary.Add("id2", "some other value");
dictionary.Add("id3", "another value");
string value = dictionary["id2"];
} Data Structures Visualization Diagrams
"Custom" Made Structures
Linked List
Note: There are a few types of linked lists:
- > In a regular linked list each element contains a value and the pointer to the next element.
- > In a circular linked list, the last element points to the first element making a loop.
- > In a doubly linked list, an element has two pointers, one pointing to the previous element and one pointing to the next element. This allows us to move back and forth the elements in the list without having to loop over the entire list again.
MyList<int> list = new MyList<int>(); list.Add(8); list.Add(7); list.RemoveAt(0);
Linked List Implementation Code
public class MyList<T>
{
//////////////////////// List properties ////////////////////////
public Node<T> rootNode { get; set; } = null; //Reference to the first node.
public Node<T> currentNode { get; set; } = null; //Reference to the last added node.
////////////////////////////////////////////////////////////////
////////////////////// Node class model ////////////////////////
public class Node<T>
{
public Node(T data)
{
Value = data;
Next = null;
}
public T Value { get; set; }
public Node<T> Next { get; set; }
}
////////////////////////////////////////////////////////////////
////////////////// List Manipulation Methods ////////////////////
public void Add(T data)
{
//Create a new node with the provided data.
Node<T> newNode = new Node<T>(data);
//Set the root node to the new node if the list is empty.
if(rootNode is null)
rootNode = newNode;
//Set the next node reference of the current node to the newly created node.
if(currentNode is not null)
currentNode.Next = newNode;
//Update the current node of the list to the new node.
currentNode = newNode;
}
public void Remove(Node<T> removeNode)
{
if (removeNode is null)
return;
Node<T> current = rootNode;
Node<T> prev = null;
//Find the node to be removed.
while (current is not null && current != removeNode)
{
prev = current;
current = current.Next;
}
//"Bypass" the current node. After there is no reference is left to it, it will be removed by the garbage collector.
prev.Next = current.Next;
//Set the current node of the list to the last node.
if (current.Next is null)
currentNode = prev;
}
public void RemoveAt(int removeAtIndex)
{
if (removeAtIndex < 0)
throw new IndexOutOfRangeException("Index out of range.");
//Start at the beginning of the list and iterate over the list till we get to the index.
Node<T> current = rootNode;
Node<T> prev = null;
for (int i = 0; i < removeAtIndex; i++)
{
prev = current;
current = current.Next;
if (current is null)
throw new IndexOutOfRangeException("Index out of range.");
}
if (prev is null) //If removing first element.
{
rootNode = current.Next;
currentNode = rootNode;
}
else if (current.Next is null) //If removing last element.
{
currentNode = prev;
currentNode.Next = null;
}
else //If removing element in the middle.
{
//"Bypass" the current node. After there is no reference left to it, it will be removed by the garbage collector.
prev.Next = current.Next;
}
}
public T Get(int index)
{
if (index < 0)
throw new IndexOutOfRangeException("Index out of range.");
//Iterate over list to find the node.
Node<T> current = rootNode;
for (int i = 0; i < index; i++)
{
current = current.Next;
if (current == null)
throw new IndexOutOfRangeException("Index out of range.");
}
return current.Value;
}
public Node<T> GetNode(T value)
{
//Iterate over list to find the node.
Node<T> current = rootNode;
while (current != null)
{
if (EqualityComparer<T>.Default.Equals(current.Value, value))
return current;
current = current.Next;
}
return null;
}
//Additionally we could implement an indexer allows us to use [] to access elements in the list.
//More about indexers here: https://eecs.blog/c-indexers/
////////////////////////////////////////////////////////////////
} Queue
A queue contains elements in a FIFO(first in first out) order. You can only add elements to the back of the queue(using Enqueue()) and remove elements from the front of the queue(using Dequeue()).
A queue is really just a list with some restrictions on how you can interact with it. The restrictions are that you can only add elements to the front of the list and remove them from the back.
MyQueue<int> queue = new MyQueue<int>(); queue.Enqueue(1); queue.Enqueue(5); queue.Enqueue(3); int queueItem = queue.Dequeue();
Queue Implementation Code
public class MyQueue<T>
{
//////////////////////// Queue properties ///////////////////////
internal Node<T> rootNode = null; //Reference to the first node.
internal Node<T> currentNode = null; //Refference to the last added node.
////////////////////////////////////////////////////////////////
////////////////////// Node class model ////////////////////////
public class Node<T>
{
public Node(T data)
{
Value = data;
Next = null;
}
public T Value { get; set; }
public Node<T> Next { get; set; }
}
////////////////////////////////////////////////////////////////
///////////////// Queue Manipulation Methods ///////////////////
public void Enqueue(T data)
{
//Create a new node with the provided data.
Node<T> newNode = new Node<T>(data);
if (rootNode is null) //... set the root node to the new node if the queue is empty.
{
rootNode = newNode;
currentNode = newNode;
}
else //... add the new node to the end of the queue.
{
//Set the next node reference of the current node to the newly created node.
currentNode.Next = newNode;
//Update the current node of the list to the new node.
currentNode = newNode;
}
}
public T? Dequeue() //the ? is used to allow the return of null for type T.
{
if (rootNode is null)
return default(T); //Return the default value of type T if the queue is empty.
//Get the value of the first node in the queue.
T value = rootNode.Value;
//Set the root node to the next node in the queue.
rootNode = rootNode.Next;
return value;
}
////////////////////////////////////////////////////////////////
} Stack
A stack contains elements in a LIFO(last in first out) order. You can only add elements to the top of the stack(using Push()) and remove elements from the top of the stack(using Pop()).
A stack just like a queue is also really just a list with some restrictions on how you can interact with it. The restrictions being that you can only add elements to the front of the list and also only remove them from the front(you could also do the opposite and only add/remove elements from the back).
MyStack<int> stack = new MyStack<int>(); stack.Push(1); stack.Push(5); stack.Push(3); int stackItem = stack.Pop();
Stack Implementation Code
public class MyStack<T>
{
/////////////////////// Stack properties ///////////////////////
internal Node<T> currentNode = null; //Reference to the last added node.
////////////////////////////////////////////////////////////////
////////////////////// Node class model ////////////////////////
public class Node<T>
{
public Node(T data)
{
Value = data;
Previous = null;
}
public T Value { get; set; }
public Node<T> Previous { get; set; }
}
////////////////////////////////////////////////////////////////
///////////////// Stack Manipulation Methods ///////////////////
public void Push(T data)
{
//Create a new node with the provided data.
Node<T> newNode = new Node<T>(data);
if (currentNode is null)
{
//Set the root node to the new node if the list is empty.
currentNode = newNode;
}
else
{
//Set the previous node reference of the new node to the current node.
newNode.Previous = currentNode;
//Update the current node of the list to the new node.
currentNode = newNode;
}
}
public T? Pop() //the ? is used to allow the return of null for type T.
{
if (currentNode is null)
return default(T); //Return the default value of type T if the queue is empty.
//Get the value of the last node on the stack.
T value = currentNode.Value;
//Set the current node to the node previous node of the last node in the stack.
currentNode = currentNode.Previous;
return value;
}
public T? Peek() //the ? is used to allow the return of null for type T.
{
if (currentNode is null)
return default(T); //Return the default value of type T if the queue is empty.
//Get the value of the last node on the stack and return it without removing the current node.
return currentNode.Value;
}
////////////////////////////////////////////////////////////////
} Tree
//Declare/instantiate a tree ... Tree<int> tree = new Tree<int>(); //... and add nodes to it. tree.Root = new Tree<int>.Node<int>(1); var node2 = new Tree<int>.Node<int>(2); var node3 = new Tree<int>.Node<int>(3); tree.Root.AddNode(node2); tree.Root.AddNode(node3); var node4 = new Tree<int>.Node<int>(4); node3.AddNode(node4); var node5 = new Tree<int>.Node<int>(5); var node6 = new Tree<int>.Node<int>(6); node4.AddNode(node5); node4.AddNode(node6); tree.BFS(Console.WriteLine); tree.DFS(Console.WriteLine);
Tree Implementation Code
public class Tree<T>
{
///////////////////////// Constructors /////////////////////////
public Tree(Node<T> rootNode = null)
{
Root = rootNode;
}
////////////////////////////////////////////////////////////////
//////////////////////// Queue properties ///////////////////////
public Node<T> Root { get; set; }
////////////////////////////////////////////////////////////////
////////////////////// Node class model ////////////////////////
public class Node<T>
{
public Node(T value)
{
Value = value;
Children = new List<Node<T>>();
}
public T Value { get; set; }
public List<Node<T>> Children { get; set; }
public void AddNode(T value)
{
Children.Add(new Node<T>(value));
}
public void AddNode(Node<T> node)
{
Children.Add(node);
}
public void RemoveNode(Node<T> node)
{
Children.Remove(node);
}
}
////////////////////////////////////////////////////////////////
////////////////// Tree Manipulation Methods ///////////////////
public Node<T> Find(T value)
{
return FindNodeWithValue(Root, value);
}
private Node<T> FindNodeWithValue(Node<T> node, T value)
{
if (node == null)
return null;
if (EqualityComparer<T>.Default.Equals(node.Value, value))
return node;
//Recursively iterate the children and look for the value.
foreach (var child in node.Children)
{
var result = FindNodeWithValue(child, value);
if (result != null)
return result;
}
return null;
}
//Breadth First Search - Done non-recursively using a queue.
public void BFS(Action<T> action)
{
if (Root == null)
return;
Queue<Node<T>> queue = new Queue<Node<T>>();
queue.Enqueue(Root);
//Iterate through the queue and process each node until the queue is empty.
while (queue.Count > 0)
{
//Get the current node from the queue.
Node<T> node = queue.Dequeue();
//Process the current node with the function passed in via the action parameter.
action(node.Value);
//Add the children of the current node to the queue.
foreach (var child in node.Children)
queue.Enqueue(child);
}
}
//Depth First Search - Done non-recursively using a stack.
public void DFS(Action<T> action)
{
if (Root == null)
return;
Stack<Node<T>> stack = new Stack<Node<T>>();
stack.Push(Root);
//Iterate through the stack and process each node until the stack is empty.
while (stack.Count > 0)
{
//Get the current node from the stack.
Node<T> node = stack.Pop();
//Process the current node with the function passed in via the action parameter.
action(node.Value);
//Add the children of the current node to the stack in reverse order.
for (int i = node.Children.Count - 1; i >= 0; i--)
stack.Push(node.Children[i]);
}
}
////////////////////////////////////////////////////////////////
} Graph
A graph is a data structure composed of nodes and edges. An edge is a connection between two nodes. Each node has a value and a list of edges(references pointing to other nodes).
A graph can be directed or undirected. The blockhain for example, is a DAG(directed acyclic graph) where nodes can only be added in one direction. In an undirected graph, the edges don’t have a direction and can point to any other node in the graph.
//Declare/instantiate a graph ...
Graph<int> graph = new Graph<int>();
//... and add nodes and edges to it.
graph.AddNode(0);
graph.AddNode(1);
graph.AddNode(2);
graph.AddNode(3);
graph.AddNode(4);
graph.AddEdge(0, 1, 1);
graph.AddEdge(0, 4, 1);
graph.AddEdge(1, 2, 1);
graph.AddEdge(1, 3, 1);
graph.AddEdge(1, 4, 1);
graph.AddEdge(2, 3, 1);
graph.AddEdge(3, 4, 1);
Console.WriteLine("BFS traversal:");
graph.TraverseBFS(0, Console.WriteLine);
Console.WriteLine("DFS traversal:");
graph.TraverseDFS(0, Console.WriteLine); Graph Implementation Code
//A graph data structure can either be represented using an adjacency list or an adjacency matrix.
//We'll use an adjacency list to represent the graph in this example.
//Adjacency list vs matrix: https://en.wikipedia.org/wiki/Adjacency_list#:~:text=of%20the%20degree.-,Trade%2Doffs,-%5Bedit%5D
public class Graph<T>
{
///////////////////////// Constructors /////////////////////////
public Graph()
{
nodes = new Dictionary<T, Node<T>>();
}
////////////////////////////////////////////////////////////////
/////////////////////// Graph properties ///////////////////////
private Dictionary<T, Node<T>> nodes;
////////////////////////////////////////////////////////////////
////////////////// Node - Edge class models ////////////////////
public class Node<T>
{
public Node(T value)
{
Value = value;
Edges = new List<Edge>();
}
public T Value { get; set; }
public List<Edge> Edges { get; }
}
public class Edge
{
public Node<T> Target { get; set; }
public int Weight { get; set; }
public Edge(Node<T> target, int weight)
{
Target = target;
Weight = weight;
}
}
///////////////////////////////////////////////////////////////
////////////////// Graph Manipulation Methods /////////////////
public void AddNode(T value)
{
if (!nodes.ContainsKey(value))
nodes[value] = new Node<T>(value);
}
public void AddEdge(T source, T target, int weight)
{
if (!nodes.ContainsKey(source) || !nodes.ContainsKey(target))
throw new ArgumentException("Source or target node doesn't exist.");
Node<T> sourceNode = nodes[source];
Node<T> targetNode = nodes[target];
sourceNode.Edges.Add(new Edge(targetNode, weight));
targetNode.Edges.Add(new Edge(sourceNode, weight));
}
public void AddDirectedEdge(T source, T target, int weight)
{
if (!nodes.ContainsKey(source) || !nodes.ContainsKey(target))
throw new ArgumentException("Source or target node doesn't exist.");
Node<T> sourceNode = nodes[source];
Node<T> targetNode = nodes[target];
sourceNode.Edges.Add(new Edge(targetNode, weight));
}
public void RemoveNode(T value)
{
if (!nodes.ContainsKey(value))
throw new ArgumentException("Node doesn't exist.");
//Remove the node from the dictionary.
Node<T> nodeToRemove = nodes[value];
nodes.Remove(value);
//Remove edges pointing to the removed node.
foreach (var node in nodes.Values)
node.Edges.RemoveAll(edge => edge.Target == nodeToRemove);
}
public bool ContainsNode(T value)
{
return nodes.ContainsKey(value);
}
public bool ContainsEdge(T source, T target)
{
if (!nodes.ContainsKey(source) || !nodes.ContainsKey(target))
return false;
Node<T> sourceNode = nodes[source];
return sourceNode.Edges.Any(edge => edge.Target.Value.Equals(target));
}
public void TraverseBFS(T start, Action<T> action)
{
//Use hashset to keep track of visited nodes.
HashSet<T> visited = new HashSet<T>();
Queue<Node<T>> queue = new Queue<Node<T>>();
Node<T> startNode = nodes[start];
queue.Enqueue(startNode);
visited.Add(startNode.Value);
//Iterate through the queue and process each node until the queue is empty.
while (queue.Count > 0)
{
//Get the current node from the queue.
Node<T> currentNode = queue.Dequeue();
//Process the current node with the function passed in via the action parameter.
action(currentNode.Value);
//Add the children of the current node to the queue.
foreach (Edge edge in currentNode.Edges)
{
if (!visited.Contains(edge.Target.Value))
{
queue.Enqueue(edge.Target);
visited.Add(edge.Target.Value);
}
}
}
}
public void TraverseDFS(T start, Action<T> action)
{
//Use hashset to keep track of visited nodes.
HashSet<T> visited = new HashSet<T>();
Stack<Node<T>> stack = new Stack<Node<T>>();
Node<T> startNode = nodes[start];
stack.Push(startNode);
//Iterate through the stack and process each node until the stack is empty.
while (stack.Count > 0)
{
//Get the current node from the stack.
Node<T> currentNode = stack.Pop();
//If the node hasn't been visited, process it and add its children to the stack.
if (!visited.Contains(currentNode.Value))
{
//Process the current node with the function passed in via the action parameter.
action(currentNode.Value);
//Mark the current node as visited.
visited.Add(currentNode.Value);
//Add the children of the current node to the stack.
foreach (Edge edge in currentNode.Edges)
{
if (!visited.Contains(edge.Target.Value))
stack.Push(edge.Target);
}
}
}
}
///////////////////////////////////////////////////////////////
} HashSet/Dictionary
A hash set/hash map is a collection of unique values with very fast lookup times for stored values. This is because it uses a hash function to map the value to a location in memory(just like an array).
A typical use case for a hash set would be iterating over a data structure and using the hash set to check if you have already visited a node. So every time you visit a node you add it to the hash set, then before you visit the next node you check if it’s in the hash set.
A dictionary is a collection of key-value pairs. It’s almost the same as a hashset with the addition of a value stored “behind” the key which can be used to look up the value said value.
MyHashtable<string, string> dictionary = new MyHashtable<string, string>();
dictionary.Add("id1", "some value");
dictionary.Add("id2", "some other value");
dictionary.Add("id3", "another value");
if (dictionary.Contains("id2"))
{
//Get value by key ...
string value = dictionary.Get("id2");
//... do something ...
//... and remove element.
dictionary.Remove("id2");
} HashSet/Dictionary Implementation Code
public class MyHashtable<K, V>
{
///////////////////////// Constructors /////////////////////////
public MyHashtable(int size = 100)
{
this.size = size;
hashtable = new LinkedList<KeyValuePair<K, V>>[size];
}
////////////////////////////////////////////////////////////////
//////////////////// Hash Table properties /////////////////////
private int size;
private LinkedList<KeyValuePair<K, V>>[] hashtable;
////////////////////////////////////////////////////////////////
/////////////////////// Hash Table Methods /////////////////////
public void Add(K key, V value)
{
if (key == null)
throw new ArgumentNullException("Key cannot be null.");
//Calculate the index for the given key and the size of the table.
//Because the key can be any type we need to use the GetHashCode() method to get a unique integer for the key.
//We then use the modulo operator to get a number between 0 and the size of the hashtable.
int index = calculateIndex(key);
if (hashtable[index] == null)
hashtable[index] = new LinkedList<KeyValuePair<K, V>>();
//Add the key value pair to the linked list at the calculated index.
//Using a list to store the values at a certain index instead of storing them directly in the hashtable array gives us
//the ability to deal with hash(key) collisions by simply adding the key value pair with the same key to the end of the list.
hashtable[index].AddLast(new KeyValuePair<K, V>(key, value));
}
public V? Get(K key)
{
if (key == null)
throw new ArgumentNullException("Key cannot be null.");
//Calculate the index for the given key and the size of the table.
int index = calculateIndex(key);
//If the index is empty, the key is not in the hashtable.
if (hashtable[index] == null)
throw new KeyNotFoundException("Key not found.");
//Iterate through the linked list of the calculated index and return the value if the key is found.
foreach (var item in hashtable[index])
{
if (item.Key.GetHashCode() == key.GetHashCode())
return item.Value;
}
throw new KeyNotFoundException("Key not found.");
}
public bool TryGet(K key, out V value)
{
if (key == null)
throw new ArgumentNullException("Key cannot be null.");
//Calculate the index for the given key and the size of the table.
int index = calculateIndex(key);
//If the index is empty return false and set the out value to the default value of the type V.
if (hashtable[index] == null)
{
value = default(V);
return false;
}
//Iterate through the linked list of the calculated index and return the value if the key is found.
foreach (var item in hashtable[index])
{
if (item.Key.GetHashCode() == key.GetHashCode())
{
value = item.Value;
return true;
}
}
value = default(V);
return false;
}
public bool Contains(K key)
{
if (key == null)
throw new ArgumentNullException("Key cannot be null.");
//Calculate the index for the given key and the size of the table.
int index = calculateIndex(key);
//If the index is empty return false.
if (hashtable[index] == null)
return false;
//Iterate through the linked list of the calculated index and return true if the key is found.
foreach (var item in hashtable[index])
{
if (item.Key.GetHashCode() == key.GetHashCode())
return true;
}
return false;
}
public void Remove(K key)
{
if (key == null)
throw new ArgumentNullException("Key cannot be null.");
//Calculate the index for the given key and the size of the table.
int index = calculateIndex(key);
//If the index is empty return.
if (hashtable[index] == null)
return;
KeyValuePair<K, V> itemToRemove = default(KeyValuePair<K, V>);
//Iterate through the linked list of the calculated index and get the key value pair to be removed if the key is found.
foreach (var item in hashtable[index])
{
if (item.Key.GetHashCode() == key.GetHashCode())
{
itemToRemove = item;
break;
}
}
//Remove the key value pair from the linked list.
hashtable[index].Remove(itemToRemove);
}
private int calculateIndex(K key)
{
//Calculate the index for the given key by hashing its value first.
//The GetHashCode() method returns a unique integer for the key. It's present in the System.Object(the data type all other data types inherit from) class.
//We could restrict the key to an integer and directly use it in the hash calculation below.
//However using a generic type and calling GetHashCode() enables us to use any type as the key.
int hashCode = key.GetHashCode();
//Calculate the index by taking the modulo of the hash code and the size of the hashtable.
int index = hashCode % hashtable.Length;
//Get the absolute value of the index to avoid negative indexes.
index = Math.Abs(index);
return index;
}
///////////////////////////////////////////////////////////////
} Sorting Algorithms
- > time and space complexities
- > iterative or recursive(use iteration or recursion for sorting)
- > comparison-based(element are compared) or non-comparison-based(instances of elements are counted)
- > in place(sort data in the original collection) or out of place(extra space needs to be allocated)
- > stable/non-stable (elements with the same keys will have their order preserved or not)
Which algorithm you choose depends on the size of the collection you want to sort, the difference between the smallest and largest number in the collection, etc.
In this section, we’ll look at a few basic sorting algorithms. When writing software in the real world 99% of the time you don’t even have to think about sorting algorithms. It depends on the type of stuff you will be working on but I have never had to write my own or even care about the type of sorting algorithms used. I mainly code in C# so I just use LINQ to sort a collection if needed.
You should just know that there are different types of sorting algorithms out there with different properties(space/time complexity, stable/non-stable, …). If you ever encounter a situation where the type of sorting algorithm used would greatly impact the performance of your code then take a more in depth look at all the possible algorithms with their pros and cons. I think it’s pointless trying to memorize a bunch of different sorting algorithms that you will probably forget as you will most likely go years without ever needing to implement or care about the type of sorting algorithm you are using.
Note: Here’s a very cool video visualizing a bunch of different sorting algorithms.
Bubble Sort
Bubble sort iterates through a list and compares adjacent elements. If they are in the wrong order the items will be swapped.
Time complexity: O(n^2)
Space complexity: O(1)
public static void BubbleSort(int[] arr)
{
if (arr is null)
throw new ArgumentNullException();
if (arr.Length == 0)
return;
//Itertate through the array.
for (int i = 0; i < arr.Length; i++)
{
//Iterate through the array and compare each element with the next element.
for (int j = 0; j < arr.Length - i - 1; j++) //-i because the last i elements are already sorted and -1 to skip the last element.
{
//If current element is greater than next element swap them.
if (arr[j] > arr[j + 1])
{
//Save current element in temp variable.
int temp = arr[j];
//Assign next element to current element.
arr[j] = arr[j + 1];
//Assign temp variable to next element.
arr[j + 1] = temp;
}
}
}
} Selection Sort
Selection sort iterates through a list and selects the minimum element in the unsorted part of the list. Then it swaps the minimum element with the first element in the unsorted part of the list.
Time complexity: O(n^2)
Space complexity: O(1)
public static void SelectionSort(int[] arr)
{
if (arr is null)
throw new ArgumentNullException();
if (arr.Length == 0)
return;
//Iterate through the array.
for (int i = 0; i < arr.Length; i++)
{
//Find the index of the minimum element in the unsorted portion of the array.
int minIndex = i;
for (int j = i + 1; j < arr.Length; j++)
{
//If the current element is smaller than the minimum found so far update minIndex.
if (arr[j] < arr[minIndex])
{
minIndex = j;
}
}
// Swap the minimum element with the first element of the unsorted portion.
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
} Insertion Sort
Insertion sort iterates through a list and moves elements to the right until it finds the correct position for the element.
Time complexity: O(n^2)
Space complexity: O(1)
public static void InsertionSort(int[] arr)
{
if (arr is null)
throw new ArgumentNullException();
if (arr.Length == 0)
return;
//Iterate through the array.
for (int i = 1; i < arr.Length; i++)
{
//Store the current element to be inserted.
int insert = arr[i];
//Set the index of the last element in the sorted portion.
int j = i - 1;
//Move elements that are larger than value to be inserted one position forward.
while (j >= 0 && arr[j] > insert)
{
arr[j + 1] = arr[j]; //Move the element forward.
j--; //Decrement the index to continue checking elements to the left.
}
//Insert value into the correct position in the sorted portion.
arr[j + 1] = insert;
}
} Counting Sort
Counting sort is a non-comparison sorting algorithm. It sorts elements by counting the number of occurrences of each unique element in the array.
Time complexity: O(n + k)
Space complexity: O(n + k)
Note: Radix sort is very similar to counting sort but is more suitable for larger numbers as it groups values by their digits. Here’s a great video series on radix sort.
public static void CountingSort(int[] arr)
{
if(arr is null)
throw new ArgumentNullException();
if (arr.Length == 0)
return;
//Get the maximum element in the array ...
int max = arr.Max();
//... and create an array to store the count of each element.
int[] count = new int[max + 1];
int[] output = new int[arr.Length];
//Count the number of occurrences of each element in the array.
for (int i = 0; i < arr.Length; i++)
{
//Get the value of the current element.
int value = arr[i];
//Use it as an index in the count array and increment the count.
count[value]++;
}
//Add the count of the previous element to the current element.
//This calculates the prefix sum of the elements in the count array.
//This will give us the position of each element in the output array.
for (int i = 1; i < count.Length; i++)
count[i] += count[i - 1];
//Place the elements in the correct position in the output array.
for (int i = arr.Length - 1; i >= 0; i--)
{
//Get the value of the current element.
int index = arr[i];
//Get the position of the element in the output array.
int outputArrPosition = count[index] - 1;
//Place the element in the correct position in the output array.
output[outputArrPosition] = index;
//Decrement the count of the element.
count[index]--;
}
//Copy the sorted array back to the original array.
for (int i = 0; i < arr.Length; i++)
arr[i] = output[i];
} Merge Sort
Mergesort is a divide and conquer algorithm that recursively divides the array into two halves, sorts them and finally then merges them back together.
Time complexity: O(n log n)
Space complexity: O(n)
public static void MergeSort(int[] arr)
{
if (arr is null)
throw new ArgumentNullException();
if (arr.Length == 0)
return;
int n = arr.Length;
if (n <= 1) //If array size is less than or equal to 1 the array is sorted.
return;
//Get middle index of the array.
int middleIndex = n / 2;
//Create two subarrays, one from start to midpoint and another from midpoint to the end.
int[] left = new int[middleIndex];
int[] right = new int[n - middleIndex];
//Copy elements from the original array to the subarrays.
//You might want to use Span<T> instead of Array.Copy. More about Span<T> here: https://eecs.blog/c-unsafe-code-pointers-stackalloc-and-spans/
Array.Copy(arr, 0, left, 0, middleIndex);
Array.Copy(arr, middleIndex, right, 0, n - middleIndex);
//Recursive calls to sort the left and right subarrays.
MergeSort(left);
MergeSort(right);
//Merge the sorted left and right subarrays back into the original array.
Merge(arr, left, right);
}
//Helper method for mergeing two sorted subarrays into one sorted array.
private static void Merge(int[] arr, int[] left, int[] right)
{
int nL = left.Length;
int nR = right.Length;
int i = 0;
int j = 0;
int k = 0;
//Compare subarrays elements from left and right and merge them.
while (i < nL && j < nR)
{
if (left[i] <= right[j])
{
arr[k] = left[i];
i++;
}
else
{
arr[k] = right[j];
j++;
}
k++;
}
//Copy any remaining elements from left subarray.
while (i < nL)
{
arr[k] = left[i];
i++;
k++;
}
//Copy any remaining elements from right subarray.
while (j < nR)
{
arr[k] = right[j];
j++;
k++;
}
}
Other Algorithms
In this section, we’ll look at some other basic algorithms. I won’t cover recursion, DFS(depth-first search) or BFS(breadth-first search) separately in this section as it was already covered in the data structures part. Non-recursive(dynamic programming) DFS and BFS was implemented in the tree data structure example using a stack and queue. Meanwhile, recursion was used for merge sort.
Linear Search
Linear search algorithm or naive search algorithm is the simplest search algorithm out there.
It simply performs a single iteration over the array and checks if the current element is the element we are looking for.
Time complexity: O(n)
Space complexity: O(1)
//Linear Search.
int[] arr = { 4, 6, 2, 8, 5 };
int find = 2;
int index = LinearSearch(find, arr);
Console.WriteLine($"Found element at {index}"); public static int LinearSearch(int find, int[] arr)
{
for (int i = 0; i < arr.Length; i++)
{
if (arr[i] == find)
return i;
}
//If the element is not found return -1.
return -1;
} Binary Search
If the array is sorted, we can use the binary search algorithm to find the element.
Binary search algorithm or divide and conquer is a much faster algorithm than linear search on a sorted array. It works by:
1. Finding the middle of the array and checking if the element we are looking for is larger or smaller than the middle element.
2. If the element is smaller than the middle element, the algorithm searches(same as step 1.) the left half of the array, otherwise it searches(same as step 1.) the right half.
Time complexity: O(log(n))
Space complexity: O(1)
//Binary search.
int[] sortedArr = { 2, 4, 5, 6, 8 };
int find = 5;
int index = BinarySearch(find, sortedArr);
Console.WriteLine($"Found element at {index}"); public static int BinarySearch(int find, int[] arr)
{
int left = 0;
int right = arr.Length - 1;
//While the left index is less than or equal to the right index.
while (left <= right)
{
//Calculate the middle index.
int middle = left + (right - left) / 2;
//If the element is found return the index.
if (arr[middle] == find)
return middle;
if (arr[middle] < find) //If the element is smaller than the middle element, search the left half ...
left = middle + 1;
else //... otherwise search the right half.
right = middle - 1;
}
//If the element is not found return -1.
return -1;
} Maximum Sum Subarray
The maximum sum subarray problem is where you are given an array of integers and you have to find the subarray(of specified size) that has the largest sum.
We’ll use the sliding window algorithm technique to solve this problem. It works by maintaining a “window” of the specified size and sliding it over the array while calculating the sum of all the items within the said “window”.
Time complexity: O(n)
Space complexity: O(1)
//Max sum of a subarray problem.
int[] numbers = { 4, 2, 1, 7, 8, 1, 2, 8, 1, 0 };
int k = 3;
int maxSum = MaxSumSubarray(numbers, k);
Console.WriteLine($"Maximum sum of a subarray of size {k}: {maxSum}"); public static int MaxSumSubarray(int[] numbers, int subArraySize)
{
int n = numbers.Length;
//Validate input. The array size must be greater than or equal to the window size and the window size must be positive.
if (n < subArraySize || subArraySize <= 0)
throw new ArgumentException("Invalid input: Array size is smaller than window size or window size is not positive.");
//Calculate the sum of the initial window.
int windowSum = 0;
for (int i = 0; i < subArraySize; i++)
windowSum += numbers[i];
//Set the initial maximum sum to the sum of the initial window.
int maxSum = windowSum;
//Now let's slide the window from left to right and update the maximum sum.
for (int i = subArraySize; i < n; i++)
{
//Slide the window by adding the next element(to the right) and removing the first(leftmost) element.
windowSum += numbers[i] - numbers[i - subArraySize];
//Update maxSum if the current window's sum is larger.
if(maxSum < windowSum)
maxSum = windowSum;
}
return maxSum;
} Two Sum
The “two sum” problem is where you are given an array(of sorted integers) and you have to find two elements within it that will add up to a specific value.
We will solve this problem by using the two-pointer technique. One pointer will point to the beginning of the array while the other pointer will point to the end. We’ll move the pointers towards each other until the sum of the elements at the pointers is equal to the target value.
Time complexity: O(n log n)
Space complexity: O(1)
//Max sum of a subarray problem.
int[] numbers = { 4, 2, 1, 7, 8, 1, 2, 8, 1, 0 };
int k = 3;
int maxSum = MaxSumSubarray(numbers, k);
Console.WriteLine($"Maximum sum of a subarray of size {k}: {maxSum}"); public static (int?, int?) TwoSum(int[] numbers, int targetValue)
{
int left = 0;
int right = numbers.Length - 1;
while (left < right)
{
//Calculate the sum of the two elements at the pointers.
int sum = numbers[left] + numbers[right];
if (sum == targetValue) //If the sum is equal to the target value, return the numbers.
return (numbers[left], numbers[right]);
else if (sum < targetValue) //If the sum is less than the target value, move the left pointer to the right.
left++;
else //If the sum is greater than the target value, move the right pointer to the left.
right--;
}
//If no pair is found.
return (null, null);
} Cycle Detection Using Floyds Algorithm
Floyds algorithm is used to detect cycles in a linked list.
It works by using two pointers, one slow and one fast, that traverse the linked list at different speeds. If there is a cycle in the linked list, the two pointers will eventually meet at the same node.
Time complexity: O(n)
Space complexity: O(1)
//Cycle detection in a linked list using Floyd's cycle detection algorithm.
MyList<int> list = new MyList<int>();
list.Add(5);
list.Add(2);
list.Add(8);
list.Add(7);
bool hasCycle = HasCycle(list.rootNode);
Console.WriteLine("Has cycle: " + hasCycle); public static bool HasCycle<T>(MyList<T>.Node<T> rootNode)
{
if (rootNode == null || rootNode.Next == null)
return false;
//Initialize the two pointers.
MyList<T>.Node<T> slow = rootNode;
MyList<T>.Node<T> fast = rootNode.Next;
//Iterate over the linked list until the fast pointer reaches the end of the list.
while (fast != null && fast.Next != null)
{
//If the two pointers meet at some point it means that there is a cycle in the linked list.
if (slow == fast)
return true;
//Move the slow pointer one step and the fast pointer two steps forward.
slow = slow.Next;
fast = fast.Next.Next;
}
//No cycle found.
return false;
} A* Path Finding Algorithm
A* algorithm is a pathfinding algorithm that is used to find the shortest path between two points on a grid. Here’s a great video explaining it.
To implement the A* algorithm you can either convert the 2D array grid into a graph node list and or iterate through the grid and generate the neighboring nodes on the fly. We’ll go with the on the fly approach.
//Find path between two points in a grid using A* algorithm.
int[,] grid = {
{ 0, 0, 0, 0, 0, 0, 1 },
{ 0, 1, 1, 0, 0, 1, 0 },
{ 0, 0, 0, 0, 1, 0, 0 },
{ 0, 0, 1, 1, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0 }
};
var start = new OtherAlgorithms.AStar.Node(0, 0);
var finish = new OtherAlgorithms.AStar.Node(2, 6);
List<OtherAlgorithms.AStar.Node> path = OtherAlgorithms.AStar.FindPath(grid, start, finish);
if (path is null)
{
Console.WriteLine("No path found.");
}
else
{
Console.WriteLine("Path:");
foreach (var node in path)
Console.WriteLine($"({node.Row}, {node.Col})");
} public static class AStar
{
public class Node //The Node will represent a cell in the grid.
{
public Node(int row, int col)
{
Parent = null;
Row = row;
Col = col;
G_Cost = 0;
H_Cost = 0;
F_Cost = 0;
}
public Node Parent { get; set; }
public int Row { get; set; }
public int Col { get; set; }
public int G_Cost { get; set; } //Distance from starting node.
public int H_Cost { get; set; } //Distance from end node.
public int F_Cost { get; set; } //F_Cost = G_Cost + H_Cost
}
/// <summary>
/// Finds the shortest path between two points on a grid using the A* algorithm.
/// </summary>
/// <param name="grid"></param>
/// <param name="start"></param>
/// <param name="finish"></param>
/// <returns></returns>
public static List<Node> FindPath(int[,] grid, Node start, Node finish)
{
//Make a HashSet to store visited nodes.
HashSet<Node> visitedNodes = new HashSet<Node>(comparer: new NodeEqualityComparer());
//The SortedSet will store the open nodes. It's similar to a HashSet but it maintains the order of the items.
HashSet<Node> openNodesSet = new HashSet<Node>(comparer: new NodeEqualityComparer());
//Add the start node to the open nodes set.
openNodesSet.Add(start);
//Iterate until the open nodes set is empty
while (openNodesSet.Count > 0)
{
//Get the node with the lowest F value from the open set.
Node current = GetLowestFCostNode(openNodesSet);
//Check if the current node is the goal. If so reconstruct and return the path.
if (current.Row == finish.Row && current.Col == finish.Col)
return ReconstructPath(current);
//Add the current node to the list of already visited nodes.
visitedNodes.Add(current);
openNodesSet.Remove(current);
//Generate the neighbouring nodes of the current node from the grid.
Node[] neighbors = GetNeighbors(grid, current);
//Iterate through each neighbor.
foreach (Node neighbor in neighbors)
{
if (neighbor == null)
continue;
//Check if the neighbor has already visited ...
if (visitedNodes.Contains(neighbor))
continue; // ... if so skip it.
//Calculate the summed G_Cost so far.
//Here each step has a cost of 1. It's however possible to assign different costs to different steps.
//For example, you could imagine the cost as the Z axis and assign a cost of 1 to a flat area and a cost of 2 or more to a slope.
int summedG_cost = current.G_Cost + 1;
//If the neighbor is not in the open set, add it.
if (!openNodesSet.Contains(neighbor))
openNodesSet.Add(neighbor);
else if (summedG_cost >= neighbor.G_Cost) //If the new G_Cost is higher than the old one ...
continue; //... this is not a better path so skip this neighbor.
//Update the neighbor.
neighbor.Parent = current;
neighbor.G_Cost = summedG_cost;
neighbor.H_Cost = CalcDistance(neighbor, finish);
neighbor.F_Cost = neighbor.G_Cost + neighbor.H_Cost;
}
}
//No path found.
return null;
}
//Get the node with the lowest F value from the open set.
private static Node GetLowestFCostNode(HashSet<Node> openSet)
{
Node lowestNode = null;
int lowestFCost = int.MaxValue;
foreach (Node node in openSet)
{
if (node.F_Cost < lowestFCost)
{
lowestFCost = node.F_Cost;
lowestNode = node;
}
}
return lowestNode;
}
//Get the neighbors of a node from the grid.
private static Node[] GetNeighbors(int[,] grid, Node node)
{
Node[] neighbors = new Node[4];
//Get the dimensions(height/width) of the grid.
int numRows = grid.GetLength(0);
int numCols = grid.GetLength(1);
//Define the 4 possible directions within the arrays.
//Then access them during the iteration. This way we can reduce the amount of code.
int[] xDir = { -1, 0, 1, 0 };
int[] yDir = { 0, -1, 0, 1 };
//Iterate through the 4 possible directions.
for (int i = 0; i < 4; i++)
{
//Calculate the new position by adding/subtracting 1 from the current node position.
int newRow = node.Row + xDir[i];
int newCol = node.Col + yDir[i];
//Check if the new position is within the grid and not blocked, else skip this neighbor.
bool isXWithinGrid = newCol >= 0 && newCol < numCols; //min. and max. check for col/x-axis.
if(!isXWithinGrid)
continue;
bool isYWithinGrid = newRow >= 0 && newRow < numRows; //min. and max. check for row/y-axis.
if (!isYWithinGrid)
continue;
bool blocked = grid[newRow, newCol] == 1; //Check if blocked.
if (blocked)
continue;
//If the neighbor is valid, create a new node and add it to the neighbors array.
neighbors[i] = new Node(newRow, newCol);
}
return neighbors;
}
//Reconstruct the path from the finish node to the start node.
private static List<Node> ReconstructPath(Node currentNode)
{
List<Node> path = new List<Node>();
while (currentNode != null) //Iterate until we reach the node without a parent(start node).
{
//Save the current node to the path list ...
path.Add(currentNode);
//... and set the current node to its parent.
currentNode = currentNode.Parent;
}
//Reverse the path to get the correct order.
path.Reverse();
return path;
}
//Calculate the shortest path between two points/nodes.
private static int CalcDistance(Node current, Node finish)
{
//Manhattan distance(straight line) is used to calculate the distance between two points on a grid.
return Math.Abs(current.Row - finish.Row) + Math.Abs(current.Col - finish.Col);
}
//Custom comparer for nodes.
class NodeComparer : IComparer<Node>
{
public int Compare(Node x, Node y)
{
if (x.F_Cost == y.F_Cost)
return 0;
if (x.F_Cost < y.F_Cost)
return -1;
return 1;
}
}
class NodeEqualityComparer : IEqualityComparer<Node>
{
public bool Equals(Node x, Node y)
{
return x.Row == y.Row && x.Col == y.Col;
}
public int GetHashCode(Node obj)
{
return obj.Row.GetHashCode() ^ obj.Col.GetHashCode();
}
}
} Dijkstra's Path Finding Algorithm
Dijkstra’s algorithm is a pathfinding algorithm that is used to find the shortest path between two points in a graph. Here’s a great video explaining it.
//Find shortest path between two points in a graph using Dijkstra's algorithm. var graph = new DijkstraExample_Graph(); graph.AddEdge(0, 1, 3); graph.AddEdge(0, 2, 2); graph.AddEdge(1, 2, 2); graph.AddEdge(1, 3, 1); graph.AddEdge(2, 3, 3); graph.AddEdge(1, 4, 4); graph.AddEdge(4, 5, 1); graph.AddEdge(3, 5, 2); graph.AddEdge(2, 5, 6); graph.AddEdge(2, 6, 5); graph.AddEdge(6, 5, 2); int startNode = 0; var (distances, paths) = graph.FindPathDijkstra(startNode); graph.PrintDistances(startNode, distances); graph.PrintPath(0, 5, paths);
public class DijkstraExample_Graph
{
//The graph is represented as a dictionary where the key is the node and the value is a dictionary of the neighbors and their weights.
private Dictionary<int, Dictionary<int, int>> graph = new Dictionary<int, Dictionary<int, int>>();
/// <summary>
/// Add an edge to the graph. An edge is a connection between two nodes with a specified weight.
/// </summary>
/// <param name="source"></param>
/// <param name="destination"></param>
/// <param name="weight"></param>
public void AddEdge(int source, int destination, int weight)
{
if (!graph.ContainsKey(source))
graph[source] = new Dictionary<int, int>();
graph[source][destination] = weight;
if(!graph.ContainsKey(destination))
graph[destination] = new Dictionary<int, int>();
graph[destination][source] = weight;
}
/// <summary>
/// Remove an edge from the graph. An edge is a connection between two nodes with a specified weight.
/// </summary>
/// <param name="source"></param>
/// <param name="destination"></param>
/// <exception cref="ArgumentException"></exception>
public void RemoveEdge(int source, int destination)
{
if (!graph.ContainsKey(source) || !graph[source].ContainsKey(destination))
throw new ArgumentException("Edge does not exist.");
graph[source].Remove(destination);
graph[destination].Remove(source);
}
/// <summary>
/// Check if an edge exists between two nodes. An edge is a connection between two nodes with a specified weight.
/// </summary>
/// <param name="source"></param>
/// <param name="destination"></param>
/// <returns></returns>
public bool ContainsEdge(int source, int destination)
{
return graph.ContainsKey(source) && graph[source].ContainsKey(destination);
}
/// <summary>
/// Find the shortest path between two nodes using Dijkstra's algorithm.
/// </summary>
/// <param name="start"></param>
/// <returns></returns>
public (Dictionary<int, int> distances, Dictionary<int, int> paths) FindPathDijkstra(int start)
{
#region Declare Variables
Dictionary<int, int> prevNodePointers = new Dictionary<int, int>();
Dictionary<int, int> distances = new Dictionary<int, int>();
HashSet<int> visitedNodes = new HashSet<int>();
//A sorted set is very similar to a hashset but it maintains the order of the items.
//For this reason we can use it for implementing a priority queue.
//A priority queue is very similar to a queue(FIFO) with the exception that the items will be sorted according to their priority.
SortedSet<(int, int)> priorityQueue = new SortedSet<(int, int)>();
#endregion
#region Initialize Variables
foreach (var vertex in graph.Keys)
{
//Initialize all distances to infinity/max value.
distances[vertex] = int.MaxValue;
//Initialize all prevNodePointers to -1;
prevNodePointers[vertex] = -1;
}
//Set the distance of the start node to 0.
distances[start] = 0;
//Add the start node to the priority queue with a distance of 0.
priorityQueue.Add((0, start));
#endregion
#region Dijkstra's Algorithm
//Iterate until the priority queue is empty.
while (priorityQueue.Count > 0)
{
//Get the node with the smallest value/priority/distance from the priority queue.
var (dist, node) = priorityQueue.Min;
//Remove the current node from the priority queue.
priorityQueue.Remove(priorityQueue.Min);
//If the node was already visited skip it. Else add it to the list of visited nodes.
if (visitedNodes.Contains(node))
continue;
else
visitedNodes.Add(node);
//Iterate through all the neighbors of the current node.
foreach (var neighbor in graph[node])
{
//Calculate the new distance.
var newDist = distances[node] + neighbor.Value;
//If the new distance is smaller than the current distance ...
if (newDist < distances[neighbor.Key])
{
//... update the distance ...
distances[neighbor.Key] = newDist;
//... add the neighbor to the priority queue ...
priorityQueue.Add((newDist, neighbor.Key));
//... and finally update the pointer to the previous node so we can reconstruct the path later.
prevNodePointers[neighbor.Key] = node;
}
}
}
#endregion
return (distances, prevNodePointers);
}
/// <summary>
/// Print the shortest distances from a specified start node to all other nodes in the graph.
/// </summary>
/// <param name="startNode"></param>
/// <param name="distances"></param>
public void PrintDistances(int startNode, Dictionary<int, int> distances)
{
Console.WriteLine($"Shortest distances from node {startNode}:");
foreach (var node in distances)
Console.WriteLine($"To node {node.Key}: {node.Value}");
}
/// <summary>
/// Prints the shortest path from a specified start node to a specified finish node.
/// </summary>
/// <param name="start"></param>
/// <param name="finish"></param>
/// <param name="prevNodePointers"></param>
public void PrintPath(int start, int finish, Dictionary<int, int> prevNodePointers)
{
List<int> path = new List<int>();
int current = finish;
//Iterate through the prevNodePointers to reconstruct the path until we reach the start node.
while (current != start && prevNodePointers.ContainsKey(current) && prevNodePointers[current] != -1)
{
path.Add(current);
current = prevNodePointers[current];
}
if (current == start)
{
path.Add(start);
path.Reverse();
Console.WriteLine($"Shortest path from {start} to {finish}: {string.Join(" -> ", path)}");
}
else
{
Console.WriteLine($"No path found from {start} to {finish}");
}
}
}